(As published in the Northeast Journal of Complex System)

Abstract

This work presents an innovative approach to understanding and measuring complexity in network models. We revisit several classic characterizations of complexity and propose a novel measure that represents complexity as an interactive process. This measure incorporates transfer entropy and Jensen-Shannon divergence to quantify both the information transfer within a system and the dynamism of its constituents’ state changes.

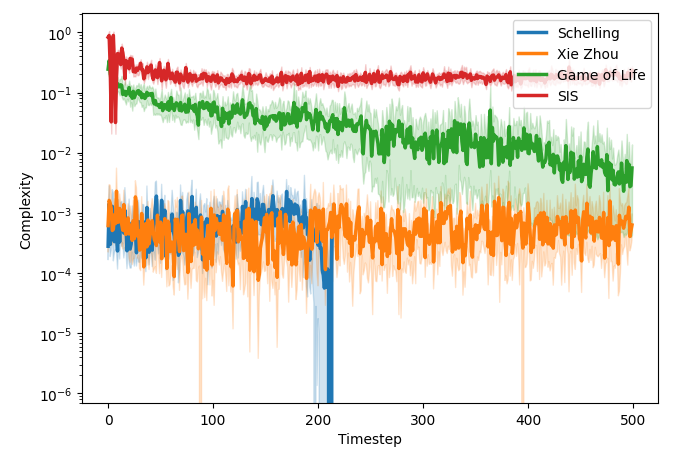
To validate our measure, we apply it to several well-known simulation models implemented in Python, including: two models of residential segregation, Conway’s Game of Life, and the Susceptible-Infected-Susceptible (SIS) model. Our results reveal varied trajectories of complexity, demonstrating the efficacy and sensitivity of our measure in capturing the nuanced interplay of interactivity and dynamism in different systems. The results corroborate the notion that heterogeneity and stochasticity increase system complexity.

This study contributes to the field by proposing a measure that not only quantifies the amount of complexity present in a system but also emphasizes the process of “complexing” marking a semantic shift from viewing complexity solely as an attribute or condition. Our findings underscore the significance of considering both interactivity and dynamism in defining and measuring complexity. The study also acknowledges limitations related to computational resources and the simplification of transfer entropy calculations, setting a clear path for future research in refining and expanding this measure of complexity.

Full text available here.